
根据今天的讨论,我们大约清楚了SHA-256算法在数字签名过程中的重要性。
用三句话来概括一下今天文章的要义:
1. SHA-256是一个安全的HASH算法,不管将哪些作为输入参数,最终得到的结果总是一个包含256个二进制位的数值。
2. 文本内容的细微变更(哪怕是一个标点符号,空白格)都会对最终加密结果有着重大的影响。
3. 如果输入的内容一模一样,那么用SHA-256函数来进行加密总是能得到相同的最终加密结果。
正式因为SHA-256函数具备这种特点,才让我们对他形成浓浓的兴趣。
由于在下边的内容中,我们又要频繁的应用到密钥的概念,这里再总结一下相关要义(但求易懂):
1. 秘钥可以简单理解为某一算法的输入参数,比如有一串数:5201314,那么我们要现今给他加密,采用一个算法f(给每一位数字+2)=7423536. 这里f就可以理解为我们的加密算法即我们这儿所说的SHA-256算法。这里的2就可以简单的觉得是我们加密的密钥。
2. 如果加密的密钥和揭秘的密钥是相同的,则该类叫对称加密法
3. 如果加密的密钥和揭秘的密钥是不相同的,那么该类就叫做非对称加密法。在非对称加密法中,用于加密的密钥称作公钥,用于揭秘的密钥称作私钥。私钥只有加密的人自己晓得,而私钥则是公开的,目的是要能让他人用私钥去进行揭秘。公钥通常是将公钥输入某个算数估算下来的,由公钥可以推导入私钥,而反之则不能。

所以,我们又可以优化一下我们之前讨论的数字签名了,前面我们说过:
SHA-256("小青欠小红10000元")的结果当作数字签名(该结果是一个包含256位二进制数的数值)。
但是,聪明的读者同学们,你们肯定可以推测得到,这还不够,一个上面不仅仅要满足对应性的需求,还要满足可分辨这个重要特点。
比如,当一个人见到一个数字签名以后,我们要确定这个是小青的签名,而不是小红,小刚,小明或则其他人的签名。但是SHA-256函数是一个公开的算法,网上有很多的在线加密,解密的工具。
比如:SHA-256("小青欠小红10000元")= 27848e760c837f0d3e31628b9f05196fd6694694d95ec158ea11f0610d5d3206。
用SHA-256函数其实可以确保和内容的对应性,确保内容不会被更改(如果被更改会导致加密结果的重大变化,详细可参见前一天的文章"数字签名")
但是,这样一直未能保证该条签名是小青签的,因为小红,小刚,小明或则任何其他人都可以用SHA-256函数进行加密得到相同的加密串。那怎么来保证该条签名是小青签名的,而不是小红,小刚,小李呢?
这里我们就用到了前面我们所说的非对称加密的算法。大概的原理是这样的:
小青用自己的公钥加密(SHA-256("小青欠小红10000元"))得到的结果就可以作为小青的签名。
小青可以将自己的私钥公布下来,这样任意一个人就可以借助小青公布的私钥对小青加密的内容进行验证了。
举个简单的反例:
小青用自己的公钥加密(SHA-256("小青欠小红10000元"))值加上自己的私钥公布下来。
小红可以借助小青公布下来的私钥对小青的数字签名进行揭秘,得到一串hash值,然后小红可以再用SHA-256("小青欠小红10000元")计算得到的hash值和前面的hash值进行对比,如果两个hash值是相同的,那么可以说明两个问题:
1. 这个签名是小青签订的,要不然不可能可以借助小青的私钥对其揭秘。
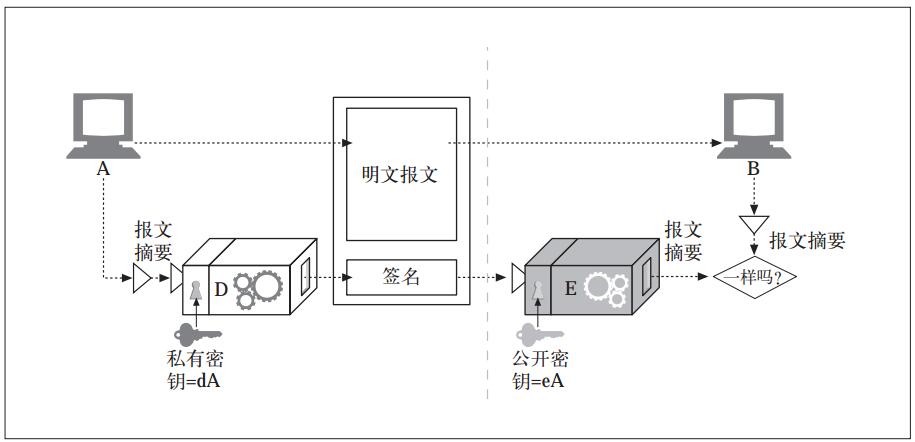
2. 这个签名的内容是"小青欠小红10000元",不然揭秘后的hash值不可能等于SHA-256("小青欠小红10000元")
经过这三天的讨论,我们可以归纳一下:
1. 数字签名和签名内容的对应性必须得到保证(这是用SHA-256函数来保证的)
2. 数字签名必须可分辨是谁签名的(可以通过非对称加密的公钥,公钥来进行辨识)
小伙伴们,你们听懂了吗?
每天学习一点点,每天进步一点点,欢迎你们关注本头条号,共同学习,共同进步。

